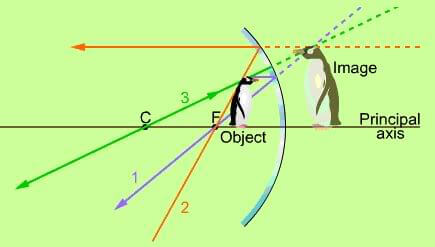
The linear magnification or magnification of a spherical mirror may be defined as the ratio of the size (height) of the image to the size (height) of the object.
The magnification of a mirror is represented by the letter m.
Thus
m = 
Or
m = 
where, h2 = size of image
h1 = size of object
As the object is always placed above the principal axis so the magnitude of h1 is always positive. But h2 can be positive or negative depending on whether the image formed is virtual or real. As the virtual image is always erect and above the principal axis therefore h2 will be positive. On the other hand, the real image is always inverted and formed below the principal axis so h2 will be negative. Thus magnification m will be positive when h2 is positive (i.e. image formed is virtual and erect) and m will be negative when h2 is negative (i.e. image formed is real and inverted).
Another point to be noted is that if the value of magnification is equal to 1, then the image formed is of the same size as that of object. If the value of magnification is more than 1, then the image formed is enlarged, and if the value of magnification is less than 1, then the image formed is diminished.
The linear magnification (m) of mirror can also be calculated in terms of image distance (v) and object distance (u), if we do not know the size (height) of object and image.
Thus
m = 
Or
m = 
where, v = image distance
u = object distance
Unit of Magnification
There is no unit of magnification (m) as it is the ratio of two similar quantities.
Test Your Understanding and Answer These Questions:
- What do you meant by linear magnification? What is its S.I. unit.
- How is linear magnification applicable in plane mirrors?
